Оптимизация транспортных издержек (часть II)
Повышение конкурентоспособности
Значительная часть логистических операций на пути движения металлопродукции от поставщика до конечного потребителя осуществляется с применением различных транспортных средств. Затраты на транспортные операции на практике составляют около 50 % от всей суммы затрат на логистические операции (под полным циклом логистики подразумеваем хранение, доставка и сбыт). Именно по этой причине оптимизация транспортных издержек становится важнейшей на пути к успеху каждого металлотрейдера. Главная цель транспортной логистики состоит в доставке продукции от множества производителей к множеству потребителей с минимальными издержками в заранее оговоренном временном интервале (точно в срок). Схематически место металлотрейдера на внутреннем рынке металла можно представить следующим образом:

Таким образом, металлотрейдер должен доставить продукцию от производителя к потребителю с минимальными транспортными издержками. Эту задачу (по минимизации транспортных издержек при перевозке) можно решить через нахождение кратчайшего пути доставки груза к потребителю. Для этого мы попробуем использовать методы, описанные нами в предыдущей статье. Рассмотрим условный пример, в котором будет три поставщика и четыре потребителя с фиксированными запасами на складах и потребностями (на практике можно использовать и гораздо большее множество контрагентов, это всего лишь увеличивает количество расчетов, но не влияет на выбор самого оптимального решения).
Суммарные запасы поставщиков в нашем случае составят 600 тонн металлопроката по тем позициям, которые запрашиваются потребителем. Потребности всех потребителей в металле не превышают 313 тонн. Таким образом, существуют избыточные запасы поставщиков в размере 287 тонн. Как видим, наш пример полностью повторяет реалии внутреннего рынка металла Украины. Мы сегодня можем наблюдать избыток предложения на рынке металла Украины, что (ввиду монопольного положения рынка), к сожалению, не всегда приводит к снижению цен.
Табл. 1. Постановка задачи о «самом кратчайшем пути».
Определение мощностей поставщиков и потребностей потребителей
| Наименование номенклатуры | Поставщики | Σ1 | Потребители | Σ2 | |||||
| 1 | 2 | 3 | 1 | 2 | 3 | 4 | |||
|
Арматура 8 (А400С), ДСТУ 3760-2006 |
120 | 50 | 30 | 200 | 10 | 8 | 26 | 11 | 55 |
|
Арматура 12 (А400С), ДСТУ 3760-2006 |
50 | 10 | 20 | 80 | 12 | 5 | 4 | 18 | 39 |
|
Арматура 32 (А400С), ДСТУ 3760-2006 |
5 | 0 | 25 | 30 | 4 | 8 | 2 | 6 | 20 |
|
Катанка 6,5, cт. 0-3пс/кп |
15 | 20 | 5 | 40 | 10 | 5 | 3 | 20 | 38 |
|
Балка 16, cт. 3сп/пс5 |
20 | 30 | 10 | 60 | 5 | 5 | 15 | 20 | 45 |
|
Круг 14, cт. 3сп/пс |
0 | 0 | 5 | 5 | 2 | 2 | 0 | 0 | 4 |
|
Лист х/к 1,5; 1,25х2,5; cт. 08кп |
15 | 15 | 30 | 60 | 10 | 8 | 10 | 10 | 38 |
|
Лист г/к 2; 1,25х2,5; cт. 3сп/пс |
20 | 5 | 40 | 65 | 0 | 15 | 5 | 15 | 35 |
|
Швеллер 12П, cт. 3сп/пс5 |
10 | 0 | 10 | 20 | 5 | 5 | 0 | 0 | 10 |
|
Уголок 45х4, cт. 3сп/пс5 |
15 | 15 | 10 | 40 | 8 | 4 | 10 | 7 | 29 |
|
Всего потребностей (запасов) |
270 | 145 | 185 | 600 | 66 | 65 | 75 | 107 | 313 |
Примечание. Σ1 — суммарные запасы поставщиков; Σ2 — суммарные потребности потребителей.
Для решения нашей задачи нам потребуются расстояния между всеми поставщиками и потребителями. Используя возможности GPS-навигации и средства картографии, вы сами сможете без труда определить расстояния между всеми вашими поставщиками и покупателями. В нашем же примере мы взяли условную матрицу расстояний.
Табл. 2. Матрица расстояний между поставщиками и покупателями
| Матрица расстояний | Поставщики | Потребители | |||||
| 1 | 2 | 3 | 1 | 2 | 3 | 4 | |
| Поставщик 1 | 20 | 30 | 15 | 30 | 60 | 35 | |
| Поставщик 2 | 20 | 60 | 30 | 20 | 38 | 35 | |
| Поставщик 3 | 30 | 60 | 37 | 46 | 57 | 21 | |
| Потребитель 1 | 15 | 30 | 37 | 10 | 12 | 32 | |
| Потребитель 2 | 30 | 20 | 46 | 10 | 34 | 21 | |
| Потребитель 3 | 60 | 38 | 57 | 12 | 34 | 24 | |
| Потребитель 4 | 35 | 35 | 21 | 32 | 21 | 24 | |
Далее попробуем определить оптимальный маршрут, используя способ нахождения самых выгодных совмещений. Напомним, что этот способ состоит в выборе маршрута, который начинается с наиболее короткого расстояния.

В нашем примере самый короткий маршрут ─ от поставщика 1 до потребителя 1 (в общей сложности его длина составит 15 км). Далее проложим путь по самому короткому пути к поставщику 2 (30 км). Поставщик 2 поставит 65 тонн потребителю 2. От потребителя 2 самый короткий путь направляет нас к поставщику 1 (30 км). Далее доставляем 75 тонн потребителю 3 и завершаем маршрут, доставив 107 тонн поставщиком 3 потребителю 4. Общая протяженность маршрута составит 233 км.
Для сравнения попробуем определить оптимальный маршрут с использованием способа исключения самых дальних расстояний.

В таблице поиска решений мы исключили (выделили крестиком) наиболее протяженные маршруты. Начальной точкой маршрута можно определить выезд от поставщика 1 в направлении потребителя 1. Далее мы возвращаемся к поставщику 1 и делаем перевозку 65 тонн потребителю 2 (благо у поставщика позволяют складские запасы). От потребителя 2 мы направляемся к поставщику 2, откуда движемся в пункт потребителя 3. Доставив партию товара потребителю 3, мы снова возвращаемся на базу поставщика 2 для загрузки и, преодолев 35 км, направляемся к потребителю 4. В рассмотренном примере протяженность пути составит 191 км. Таким образом, исключив самые дальние расстояния перевозок, нам удалось сократить общую продолжительность пути на 42 км.
Очень часто в работе металлотрейдеров возникают случаи, когда одну (из множества) перевозок нужно произвести в обязательном порядке (или в первую очередь). Причин здесь может быть несколько: клиент относится к VIP-ам, поставщик может дать выгодные условия по цене, время поставки было перенесено на более ранний или поздний срок и пр. В этом случае оптимизационная задача решается исключением складских запасов и потребностей потребителя на определенный объем. Допустим, в нашем примере, необходимо в обязательном порядке поставить 100 тонн металлопродукции от поставщика 2 к потребителю 4. Поиск оптимального пути (с использованием способа поиска самых коротких расстояний) в этом случае будет иметь такой вид:

Как и во всех предыдущих примерах, мы начинаем поставку от поставщика 1 к потребителю 1. Аналогичную поставку проводим со склада поставщика 1 к потребителю 2. Доставив 65 тонн потребителю 2, мы направимся на склад поставщика 2 (у которого запасы, ввиду обязательности поставки потребителю 4 ограничены в размере 45 тонн). Ограниченность запасов поставщика 2 вынуждает нас направиться к потребителю 4 (у которого имеются незакрытые потребности на 7 тонн). Даже невзирая на малые размеры заказа (всего 7 тонн), мы, как компания, дорожащая своим клиентом, поставляем эту партию. У нас остаются незакрытые поставки потребителю 3, которые мы обеспечиваем за счет запасов поставщика 3. В конечном итоге, общая продолжительность маршрута составит 193 км (без обязательной поставки 100 тонн потребителю 4).
Одной из разновидностей задач по оптимизации транспортных перевозок считается так называемая задача с запретами. Фактически наличие запрета означает, что поставка по некоторому каналу невозможна. На практике такие задачи встречаются довольно часто по ряду причин: у поставщика вышло из строя подъемно-транспортное оборудование, цены поставщика неприемлемы для потребителя, качество обеспечиваемой поставщиком продукции неприемлемо для потребителя. Допустим, в нашем примере поставка продукции от поставщика 3 к потребителю 4 невозможна, но заказ потребителя 4 необходимо удовлетворить. Решение задачи будет иметь следующий вид:
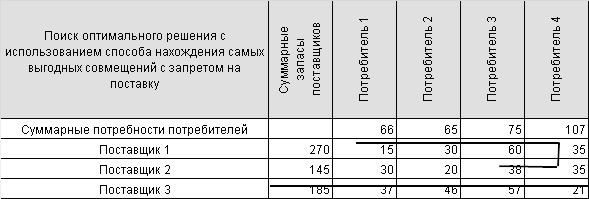
В решении задачи с запретами (с использованием способа поиска самого короткого пути) мы начнем от поставщика 1. Поставив 66 тонн потребителю 1, мы снова вернемся на склад поставщика 1 для загрузки под заказ потребителя 2. После этого мы направимся к потребителю 4 и удовлетворим его заказ с помощью запасов поставщика 1. Учитывая, что запасы поставщика (после закрытия потребностей клиентов 1, 2, 4 уменьшились до 32 тонн), мы можем удовлетворить потребности потребителя 3 только за счет поставщика 2. Общая продолжительность пути в задаче с запретами составит 198 км.
В приведенных примерах мы наглядно продемонстрировали как путем нехитрых вычислений и общедоступных способов оптимизации пути можно свести транспортные издержки к минимуму. К сожалению, на практике их не всегда удается реализовать по ряду причин:
-
загруженность транспортного пути
(наличие «пробок» на дорогах хоть и не увеличивает протяженность следования транспорта, но необратимо приводит к перерасходу топлива за счет простоя на «холостых оборотах»); -
плохое состояние дорожного пути на кратчайшем пути следования
(в этом случае наиболее короткий путь следования будет сопряжен с частыми поломками и повышенным износом транспорта); -
перевозка неоднородного товара
(задача по оптимизации транспортного пути решается оптимально, когда перевозится однородный товар (песок, уголь, мука и пр.); в металлоторговле товар разнородный, отсутствие на складе у основного поставщика нескольких тонн специфичного товара (например, калиброванного круга из спец. стали) вынудит вас сделать «крюк» на другую металлобазу, которая может располагаться на другом конце города).
В первых двух случаях наши рекомендации практически бессильны. Мы можем только рекомендовать вам при составлении матрицы расстояний учитывать загруженность и качество транспортного пути. Третий же случай обычно поддается оптимизационной коррекции. В следующей статье мы попытаемся ответить Вам на вопрос, как оптимизировать путь при перевозке разнородных продуктов (что весьма актуально для металлоторговых фирм). Кроме этого, мы рассмотрим еще один злободневный вопрос ─ как определить оптимальное время смены транспортного средства.
Дмитрий Ткалич